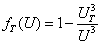In order to study the strong coupling behavior of quantum chromodynamics in the low energy region, we experimentally collide leptons with hadrons, hadrons with hadrons, and nuclei with nuclei at high speed. The initial collision produced hadron jets and bifelton pairs of heavy taste quarks. Some molecules inside the nucleus are released by high-energy collisions, forming a dense material, inheriting strong interactions and presenting elliptical flows. Thermalized quark gluon plasma. Finally, it expands and cools. In the local thermal equilibrium region, hadrons with increasingly distant interactions are formed and can be ignored, which are received by the detector. In recent years, a variety of interesting phenomena, such as P/CP parity, chiral magnetic effect (CME), chiral vortex effect (CVE) and anomalous coefficient, have appeared in large hadron physics experiments (such as RHIC and LHC), which have become the emerging theoretical focus.

It is well known that quantum chromodynamics is not suitable for perturbation in low energy regions. T 'Hooft first proposed the large N limit to study, and used the color freedom of QCD N as the expansion parameter. When N tends to infinity, the theory of strong phase interaction becomes the classical theory of weak coupling. SU(N) theory is regarded as the theory of N overlapping D branes. The feynman diagram of the perturbation expansion of SU(N) theory changes from the circle diagram on the plane to the topological expansion of the closed Riemannian surface, which corresponds to the gravitational perturbation expansion of D-film in higher dimensional space-time. As an extension of this AdS/CFT duality, gauge/gravitational duality studies the nonperturbative properties of quantum chromodynamics.

The 4-dimensional SU(N) gauge theory contains the coupling coefficient (energy scale)PNG and color degree of freedom N. 'tHooft coupling coefficient when N is infinite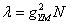Fixed. Let the adjoint field of SU(N) be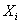，Action for

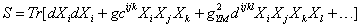
Weighing scale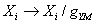后

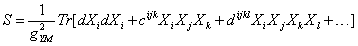
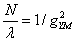
In the large N limit, the quark with SU(N) basis represents the index, which is represented by a single line, and the gluon with adjoint represents the index. Because there are generative elements, it can be regarded as the positive and negative basic representation of direct product decomposition.

Perturbation expansion of any correlation function

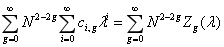
Where G is deficient. The circle chart correction is depressed by large N.

There are different low energy efficient theories for different parameter regions of the same physical system. Take D3 membrane as an example :(1) at that time, that is, far away from D3 membrane

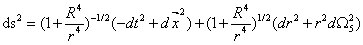
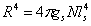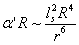，，When r is large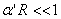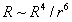（Is the curvature scalar），The metric is asymptotically flat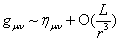（）。The action of string theory, which unfolds step by step according to curvature,

Higher-order corrections don't matter, so you get the theory of supergravity. (2) when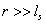, that is, when very close to D3 membrane

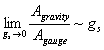
becaus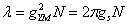e，make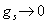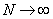，，and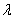Fixed finite, so the result is a pure Yang-Mills theory of gravitational decoupling. Because the curvature invariants can be evaluated directly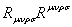in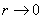Is slow, so the theory of supergravity can be extended to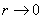，Equivalent substitution of Yang-Mills theory to achieve gauge/gravitational duality.

The supergravity theory in Bulk is analogous to the field theory with a large T 'Hooft constant on the boundary. Because when the T 'Hooft constant is large enough, in the near-horizon region near the membrane, the supergravity theory and the gauge theory on the membrane can be described independently. In other words, the Yang-Mills theory of gravitational decoupling is obtained in the large N limit. Because when bulk field takes its boundary value, the partition function of gravity is equal to that of boundary field theory,

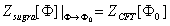
With the corresponding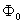The correlation function of the coupled boundary operators can be obtained from the equation of motion in BULK.

Similar to the extreme black hole solution in supergravity, the near-horizon structure of the extreme brane solution also helps to realize the gauge/gravity duality. The chan-Paton degrees of freedom at both ends of the open string can be used to realize the flavor degrees of freedom in the holographic model. Open string momentum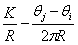，Therefore, the winding number after T duality is fractional, and the endpoints fall on different D branes. Is the open string mass spectrum with one end on the i-th D film and the other end on the j-th D film

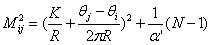
If n coincide D branes, the open chord endpoints have U(n) gauge symmetry.

Quarks have flavor and color degrees of freedom. D4 represents color film and D8 represents taste film. The low energy dynamics of D films can be described by the gauge field excited on them. D branes will have open string excitation. One end of the string is in the D4 color film, one end is in the D8 taste film, and the resulting canonical field degree of freedom is exactly

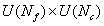The fundamental representation of a group that may represent a quark. The antiquarks are D4 and D8 branes.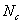A quark makes a baryon. Field theory in。

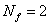Because there is no direction perpendicular to both D4 and D8 branes, dual field theory quarks are massless. The background of supergravity needs to be in a certain direction of D4 film, where the fourth dimension is selected for compactification. D4 occupies the first 4 dimensions and obtains antiperiodic boundary conditions for Fermions on compact dimensions. So supersymmetry is completely broken. Low energy supergravity can be described in the near-horizon region by classical gravity theory in BULK or gauge theory on membrane.

D0-d4 solution of Type IIA supergravity in Einstein framework,

,,

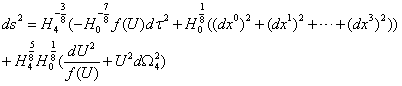
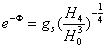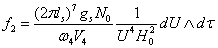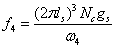
Among them

     ，    ，       

     ,              

     .                

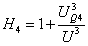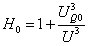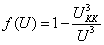
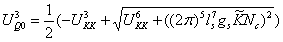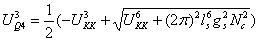Telescopic son

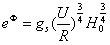
Usually take the non-vacuum part of the telescopic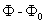。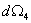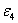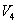，，和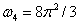They are unit four-dimensional spheres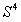, the volume form of unit four-dimensional sphere, the world volume of D4 film and the volume of unit four-dimensional sphere.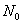和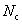Represents the number of D0 membrane and D4 membrane respectively. String parameters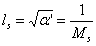。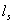Is the chord length，It's the string mass scale. I,j refers to the three dimensions of 1, 2 and 3, (1+3) and peacekeeping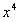And U constitutes the class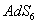.And then the last term is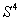.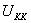It's the radius of the event horizon。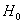,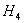They're all Harmonic functions, and they're all to the third power representing the D0 brane dispersion (on the D4 brane) in three dimensions of space. The density of the D0 membrane is shown here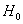In the water. And do the membrane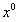And U, the singularity is within the horizon,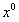It's periodic. It's time.

Let's say R is much, much bigger than R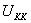，U in the horizon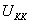Near, that is, near horizon. After doing double Wick rotation in time and compactness dimension, the form under the string frame:

，

，，

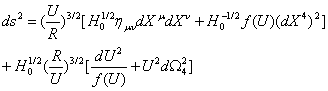
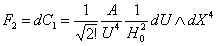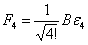
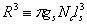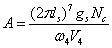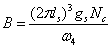
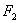The field strength is generated by a D0 membrane coupled 1-form gauge field, which is a flow on a 2-dimensional sphere. We get A and B from the equation of motion.

，

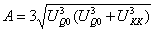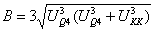
Kaluza-klein mass parameters

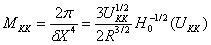
So that's the d0-D4 bubble background metric. There is also a D0-D4 black film background metric. exchange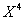with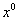，Near horizon form under string frame:

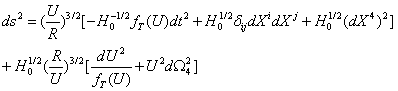
Among them