摘要：该文提出将经典阻抗控制器与模糊预测算法相结合的方法。该算法计算提供给阻抗控制器的最佳虚拟轨迹。这种控制策略允许以简单的方式在控制设计中包含由非线性模型表示的非刚性环境。从而，提高了全局力控制性能。为了减少优化参考位置的振荡，力控制策略中包括模糊缩放机。对实验性二自由度机器人的力控制方案的性能进行了说明。模糊预测算法的实时实现表明，在力控制方面比经典的力控制算法具有更好的性能。

1  简介

       如今，新材料的开发，机器人机械手机械设计的改进和更快的微处理器强调了在新一代工业机器人中应用更复杂的控制算法的必要性。高级控制算法的实现和验证需要在硬件和软件方面具有灵活的结构。该设备对于研究和分析控制器的性能至关重要。然而，测试新的力/位置控制算法的主要困难之一依赖于缺乏可用的商用开放式机器人控制器。事实上，工业机器人配备了具有固定控制规律的数字控制器，通常是PID型，不可能修改控制算法以提高其性能。通常，机器人控制器使用特定语言进行编程，例如VAL+，具有固定编程命令，具有内部定义的路径规划器，轨迹插值器和滤波器以及其他功能。而且，一般来说，这些控制器只处理位置和速度控制，这不足以在需要获得准确的力/位置跟踪性能时。

       传统上，工业机器人任务通常与操纵有关，这只需要控制手臂的位置，但其他任务，如组装、推动和抛光，需要机械手的末端执行器与环境之间的相互作用。这一事实导致有必要控制机器人和环境之间的相互作用力，从而开发更复杂的力控制算法。尽管文献中提出了许多不同的控制方案，但主要的力控制方法可以分为混合控制或阻抗控制。混合控制将机器人力任务分为两个子空间，一个力控子空间和一个位置控制子空间，然后为每个子空间设计两个独立的控制器。另一方面，阻抗控制并不明确地控制力，而是控制力与与环境接触的末端执行器的位置之间的关系。此外，当需要力跟踪时，可以计算虚拟轨迹以在环境中应用所需的力分布。这种方法很有吸引力，因为它能够以低计算负担实时有效地应用力控制算法。

       本文通过使用模糊缩放机提出了这个问题的可能解决方案，该机器使用一组自适应的离散替代方案，基于Sousa and Setnes（1999）中提出的模糊准则的满足。将模糊缩放机推广到模型预测算法并应用于力控制，缓解了模型预测算法中待求解的非凸优化问题离散化的影响。在本文中，模糊缩放机基于满足应用于力控制的模糊准则，使用一组自适应离散替代方案，在非线性环境中导出阻抗控制器的虚拟参考。进一步，提出了该算法的实时实现方法。

2  建模和力控制

2.1 建模

       考虑一个受环境接触约束的n连杆刚性关节机械手。完整的动态模型在de Witt, Siciliano, and Bastin (1997)描述：

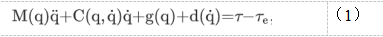
       这里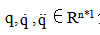分别对应于关节位置、速度和加速度矢量，M(q)∈Rn*n是对称的正定惯性矩阵，C(q,q.)∈Rn*1是向心矩阵和科里奥利矩阵，g(q)∈Rn*1包含引力项，以及d(q)∈Rn*1考虑摩擦项。向量r∈Rn*1是关节输入扭矩矢量和r。∈Rn*1表示环境施加在末端执行器上的关节扭矩的广义矢量。从(1)可以推导出笛卡尔空间中的机器人动力学模型：

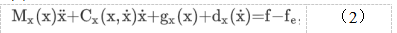
      这里x是机械手末端执行器的位置和方向的n维向量，f=J-T(q)Te∈Rn*1是接触力矢量和J表示雅可比矩阵。接触力矢量可以分解为法向项和切向项：fe=[fnft]T.法向接触力fn可以简单地表示为:

      其中k是刚度系数，δx是穿透深度，定义为δx=x-xe,切向接触力ft由于表面摩擦被认为是Yao and Tomizuka (1995)给出的:

      这里X.p是无约束或滑动速度分量，μ是末端执行器和接触面之间的干摩擦系数。

2.2 力控制

       本节介绍阻抗控制方法，以获得在非刚性环境中具有力跟踪能力的力控制方案。在这种控制方法中，操纵器和环境之间的动态关系受到控制。设二阶阻抗模型由下式给出：

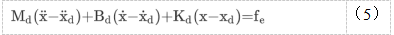
       这里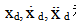和分别是所需的位置、速度和加速度，而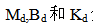d分别是在笛卡尔空间中定义的所需惯性、阻尼和刚度对角矩阵。机械手的参考或目标末端执行器加速度ut然后由：

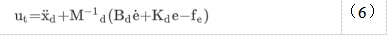
      这里e=xd-x和e.=x.d-X分别是位置和速度误差。参考资料ut可用作内回路控制器的驱动信号，以控制对环境的接触力。得到以下控制律：

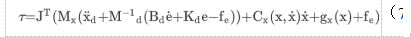
      适用于自由运动或受限运动。

      如果假设（7）中有一个重要的简化，则有可能获得Ma=M.此外，还可以考虑准静态条件，这意味着速度x≈0和q≈0.这是一个合理的近似值，因为力控制任务通常在低速执行。

      因此，得到以下简化的阻抗控制定律：

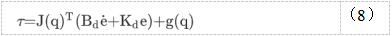
      这种控制方案等效于具有重力补偿的比例导数笛卡尔位置控制定律。可以证明对于恒定参考xd且不与环境接触，渐近稳定性x获得（deWitt等人，1997）。当末端执行器与环境接触时，接触力与零不同，无法保证渐近稳定性xd,在这种情况下，获得稳态平衡情况，可以通过Kd-1,因此，当末端执行器与环境建立完全接触时，可以进行稳定性分析，假设。

       接触面被建模为刚度为的线性弹簧。e在这种情况下，当x>o时，末端执行器处出现反作用力。然后，当机械手与环境处于稳态接触状态时，由(3)给出法向接触力，达到以下稳态平衡条件：

      闭环系统（10）中给出的平衡点在全局上是渐近稳定的，如de Witt等人（1997）所示。考虑稳态位置和力，分别在中给出所需的接触力 fd可以应用于环境。通过计算虚拟或参考位置x同时实现所需的阻抗v在约束方向上，由下式给出：

      此外，有可能获得xv从 Fd和δx，通过考虑未知环境的特征（Jung & Hsia，1995）。在这种情况下，通过替换ke在（12）中，获得以下目标轨迹：

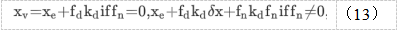
       这适用于接触和非接触条件。虚拟速度，可以通过x的数值微分获得，然而，由于接触力测量中通常出现的高频噪声，假定为零。 

       控制定律(8)可用于在考虑矢量给出的虚拟参考的情况下对环境施加所需的接触力xt=[XvXa]T，在控制定律(8)中使用该目标矢量允许在没有明确了解环境刚度系数的情况

       下进行力跟踪能力。为了提高力跟踪精度，可以在(8)中增加一个积分控制动作，得到：

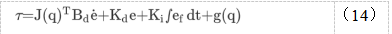
       在此控制器中的位置e=Xt-X和è=X.t-X.被重新定义为虚拟位置和速度误差，以及ef=fd-fe是强制错误。

       实时实现力跟踪的阻抗控制算法是，的简化版本。因此，对于每个采样周期T,通过以下步骤描述所实现的控制算法：

第1步：计算笛卡尔位置和速度，x(k)和(k)分别。

第2步：计算法向接触力fn(k）。

第3步：计算xv(k）在约束方向。

第5步：计算笛卡尔空间中的控制动作：

2.3混合控制算法

       这种经典的力控制算法（Raibert&Craig，1981）使用选择矩阵S=diag(s)j=1,.,m时，通过属性“1”强制子空间和“o”来定位子空间来分隔位置子空间和力子空间。矩阵S用于表示力控制方向和矩阵I-S表示剩余的位置控制方向，其中I是单位矩阵。在该算法中，控制力f(k)=[ff(k)fp(k)]T由:

      其中，无约束空间和约束空间控制律的实际实施分别由：

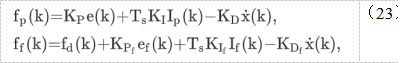
      其中ef在（17）和I中定义p是（20）中表示无约束方向的项。

      系数 KP，KI和KD是位置的PID控制器的参数，KPf，KIf和KDf是力PID控制器的参数。术语 If(k） 定义为:

        请注意，速度阻尼包含在约束方向的控制定律中，如Mandal和Payandeh（1995）所述。

3  结论 

       该文提出一种集成模型预测算法和阻抗控制器的力控制方案，用于非刚性环境。MPA使用模糊缩放机来缓解B&B算法所需的输入离散化所带来的问题。推导了模糊预测算法的实时实现，该算法使用离线计算的最优虚拟轨迹。将实验结果与其他经典控制技术（即经典阻抗控制和混合控制）进行了比较。与其他控制器相比，所提出的模糊预测算法具有更准确的力跟踪行为。未来的研究将集中在模糊预测算法的在线实现上，以便将所提出的算法扩展到具有两个以上关节的机器人。还将研究接触面撞击情况的实验研究。