摘要：在传统的分布式功率控制(DPC)算法中，对系统中的每个用户都采用相同的处理方法，即对系统中的每个用户都采用相同的功率控制算法。在本文中，我们根据用户的不同将用户划分为不同的组，并使用不同的DPC。不同的DPC算法都有自己的优点和缺点，我们的目的是“结合”不同DPC算法的优点，所以我们使用了软计算技术。在仿真结果中，我们选择了的Foschini和Miljanic的算法，该算法收敛速度较快，但对时变链路增益变化和CIR估计误差的鲁棒性较差;还采用了Kim的固定步长算法，该算法具有鲁棒性，但收敛速度较慢。利用软计算技术将这两种算法结合在一起，得到的算法收敛速度快，鲁棒性好。

关键词：分布式功率控制算法；软计算；神经模糊系统；蜂窝式无线电系统 

1 引言

      有效的发射机功率控制对于高容量蜂窝无线电系统至关重要。自Zander的集中式和分布式CIR平衡工作以来，功率控制(PC)问题受到了广泛关注。

      Grandhi等进一步研究了载波干扰和噪声比(CIR)平衡。在中，Foschini和Miljanic提出了一个更一般、更现实的模型，其中考虑了接收机噪声和各自的目标。Foschini和Miljanic的分布式算法(FMA)可以同步或异步收敛到可行系统的一个固定点。

      Grandhi等在FMA的基础上提出了分布式约束功率控制算法(DCPC)。DCPC算法已经成为学术界最广泛接受的算法之一。同时，Yates提出了广义上功率控制的收敛框架，Huang和Yates对该框架进行了扩展，结果为设计和分析新算法提供了一个框架。

      这些传统的分布式功率控制算法(DPCA)，包括许多其他算法，以相同的方法对待系统中的每个移动设备，即它们对系统中的每个用户应用相同的DPCA。在本文中，我们将移动设备划分为Z个组，在每个组中分配一个不同的DPCA，并利用软计算技术“结合”不同DPCA的优点。

      为了预测或计算蜂窝无线电系统的功率控制增量，模糊逻辑控制技术被应用于蜂窝无线电系统的闭环功率控制中。在本文中，我们采用模糊逻辑技术实现于不同的目的，即结合不同的DPCA。

      本文组织结构如下:PC问题在第2节中描述。第三节介绍了所提出的算法。第4节给出模拟结果，第5节给出结论。

2 功率控制问题

      参考一个蜂窝无线电系统，其中N个移动设备共享同一个频道。在一般情况下，我们只考虑上行链路的情况(从移动设备到基地)，并假设移动设备i在那一刻被分配给基站i。

      进一步，我们假设，如果基站i处的CIR不小于给定的目标值，则移动设备i的信号将被正确接收。这在数学上是由：

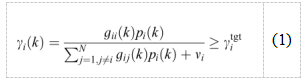
      其中pi为移动设备i的传输功率，gij为移动设备j到基站i的链路增益，包括路径损耗、阴影、多径衰落以及CDMA传输[17]的扩频/处理增益，vi为基站i的接收机噪声。以链路增益为项的矩阵。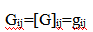称为连杆增益矩阵。一般来说，我们定义归一化链路增益矩阵H为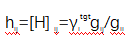，并假设它在其平均值附近随时间变化，如下所示:

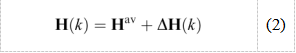
      其中Hav(已知或估计)是矩阵H的平均值，ΔH(k)(未知)根据给定的分布在每次迭代中随机变化。

把(2)代入下式：

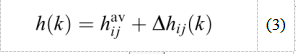
      在整个论文中，我们研究了截断功率控制[4]的情况，即PC被用来补偿超过一定的截止衰减深度的链路增益。在DSCDMA系统中，用PC来补偿深衰落会降低性能(系统容量)。我们假设收发器系统有一些处理信道中小范围多径衰落的方法，如编码、交织、分集等。

设PC补偿的链路增益间隔为:

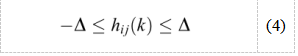
      换句话说，PC被用来补偿-Δ和Δ之间的时变链路增益。

      将(1)以矩阵形式写出γi(k)=γitgt的平均归一化链路增益和归一化噪声:

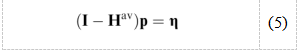
       其中p是功率矢量，Hav是(已知或估计的)平均归一化链路增益矩阵，g是噪声矢量。

       一个完全分布式PC问题定义为如何仅使用局部测量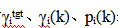来改变功率向量项pi;)，以便功率向量收敛到(6)中的最优值。

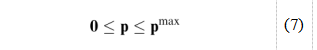
      其中pmax项为移动的最大传输功率。

3 软计算PC算法

       在传统的功率控制算法中，系统中的每个用户都被以相同的方法控制，即系统中的每个移动设备都采用相同的PC算法。然而，本文提出的算法将移动设备根据其信道条件分为不同的组，并为每个组分配不同的DPCA。软计算PC (SCPC)的一般形式见(8)

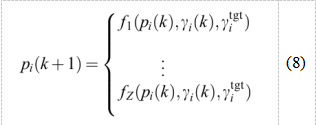
3.1 基于RBFN的SCPC设计

       在过去的三十年中，RBFN一直是神经模糊系统的研究重点所在，其目标是结合神经网络和模糊控制的优势。在[13]中，证明了RBFN的函数等于一个模糊系统。这种等价性使我们能够在闭环PC操作的背景下结合模糊系统和神经网络的优势。具有一个输出的RBFN实现了(9)中的输入输出关系。

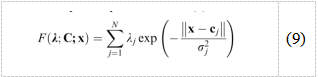
       使用“局部变量”(即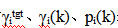)，利用“专业知识”建立了在给定信道条件下选择最佳DPCA的初始模糊规则集。利用RBFN的神经-模糊等价性，在不同衰落信道条件的训练中，集中使用神经网络技术优化这些模糊规则[9,13]。

       以下方程用于优化RBFN参数的代价参数

       在DPCAs中选择的初始模糊规则一般为(14)式。

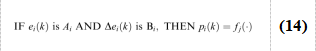
       其中Ai和Bi是变量(例如“大”，“小”等)，N是模糊规则的数量，Z是使用的DPCAs的数量。初始化最好是基于“专业知识”。

       通过梯度下降型算法使RBFN参数最小化后，由于RBFN与模糊系统的功能等价，我们得到了优化的模糊规则。

       就SCPC的稳定性而言，由于我们设想了的这个系统所使用的每个DPCA对于任何初值都收敛到不动点，因此可以直接表明整个系统也收敛到不动点。

3  结论与展望

       在“标准”分布式功率控制算法中，系统中的每个终端都使用相同的PC算法。在本文中，我们建议根据终端的信道条件将其划分为不同的组，在每个组中分配一个“合适的”DPCA，以便“结合”不同DPCA的优点。

分析该方法在不同移动速度下的性能是一个值得关注的工作。