1  引言

      为永磁同步电机(PMSM)由于其结构简单、效率高、可靠性等优点，已广泛应用于数控机床、医疗仪器、仪器仪表、航空航天等领域。目前，比例积分微分(PID)控制器由于其实现简单，在永磁同步电动机传动中仍有应用。然而，永磁同步电机系统是非线性、时变的、复杂的同时有不可避免和不可测量的干扰以及参数变化。传统的PID控制算法很难对永磁同步电动机实现令人满意的高性能控制。近年来，非线性控制方法多种多样，如自适应控制、鲁棒控制、模型预测控制等，模糊控制，和滑模控制，已经广泛应用以提高PMSM驱动器系统性能。

      在这些控制方法中，SMC被认为是提高永磁同步电动机系统抗扰性和鲁棒性最有效的方法之一。由于常规线性滑模的系统误差不能在有限时间内收敛，阻碍了其在实际工程中的应用，在滑模面中引入非线性项，使系统跟踪误差在有限时间内达到平衡点。然而，TSMC在平衡点附近仍然存在奇点问题。为了解决上述问题，我们提出了一个非奇异TSMC。分数阶形式的SMC控制系统不仅具有良好的控制性能，而且对外部负载扰动和参数变化具有鲁棒性。将SMC的收敛过程分为趋近模态阶段和滑模态阶段。除此之外还提出了等速趋近率、指数趋近率、幂函数趋近率等，提高了逼近运动的动态质量。之后，将趋近律推广到离散时域，受到国内外学者的广泛关注。但这些趋近律不能平衡收敛速度和抖振的矛盾。为了提高被控系统的鲁棒性，提出了一种无开关型趋近律。对永磁同步发电机(PMSG)的SMC采用了增强的指数趋近律。所提出的趋近律可以有效地降低系统的抖振和总谐波失真。

       在实际应用中，在控制器的基础上增加前馈补偿部分是提高系统抗干扰性能的另一种有效方法。值得注意的是，前馈补偿的质量直接受到扰动观测器性能的影响。因此，扰动观测器的相关理论近年来受到越来越多的关注。为了减小时变负载扰动对永磁同步电机控制系统的影响，本文提出了以转速和负载转矩为状态变量的负载转矩扩展滑模观测器(ESMO)。

       对负载扰动进行估计，抑制SMO的抖振。提出了一种解决永磁同步电动机驱动系统时变参数和扰动的互补SMC方案，这种新的速度控制器采用带扰动观测器的超螺旋滑模控制器设计。除此之外，提出了一种简单的自适应电流扰动观测器，用于估计永磁同步电机控制系统的时变特性和高带宽特性。此外，针对系统参数的变化会降低永磁同步电动机的抗干扰性能，在设计了高速滑模观测器。提出了一种扩展状态观测器来估计和补偿系统扰动。在传统指数逼近律的基础上增加终端开关增益项，设计饱和函数代替开关函数。仿真结果表明了该方法的有效性。我们设计了一种实用的离散分数阶终端滑模变结构速度控制器。实验结果表明，控制系统的动态性能得到了改善。

      为了减少非奇异快速终端滑模控制器(NFTSMC)的抖振，提高其动态性能，提出了一种具有新的滑模趋近律(NSMRL)的改进型快速终端滑模控制器。NSMRL能动态适应系统状态和滑模曲面的变化。同时，考虑到外部扰动，特别是负载扰动对永磁同步电动机的影响，引入滑模扰动观测器(SMDO)来估计负载扰动，并将其添加到改进的永磁同步电动机输出中作为前馈补偿项。应用于永磁同步电动机的仿真和实验结果表明，该复合控制方法具有动态响应快、抗干扰性能好等特点。本文其余部分的组织如下。第二节给出了永磁同步电动机的数学模型。在第三节中，对改进后的NFTSMC进行了设计和分析。在第四部分，将设计SMDO。第五节展示了永磁同步电动机的仿真和实验结果。最后，在第六节中给出了一些结论。

2  永磁同步电机数学模型

       永磁同步电机驱动器是一个多变量、非线性、强耦合系统。为了简化分析，本文的永磁同步电机定子采用三相对称绕组，转子采用永磁结构。假设磁路不饱和，磁场在空间上呈正弦分布，忽略磁滞和涡流损失的影响，取d轴与永磁体的励磁轴一致，q轴跟随转子旋转方向，导至d轴π/2电角。在d-q坐标系下可以描述永磁同步电动机的数学模型。

      由于角速度和位置信息可以在静止参考系中提取，电机的永磁同步电机是在静止参考系中建模的。静止(α，β)坐标系下的永磁同步电机模型为

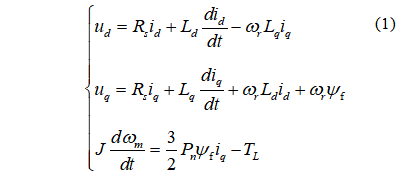
      永磁同步电动机的电磁转矩方程为：

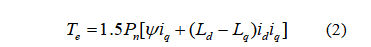
      对于表贴式永磁同步电机有：

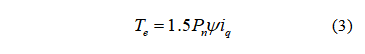
     PMSM运动方程为：

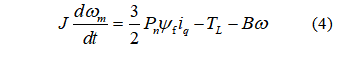
3  改进NFTSMC设计

A．参数失谐的影响

     PMSM系统的状态量定义为:

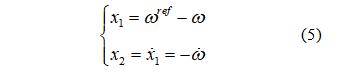
      为了便利实验设计，假设负载为0，其中：为电机给定转速：为实际转速，上式化为状态空间表达式：

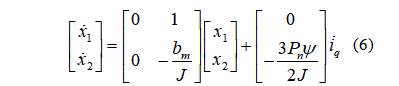
      在常规的非奇异终端滑模控制器中，滑模面设计为以下：

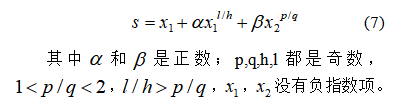
      因此，基于滑模面的控制器避免了奇异性问题。为了保证到达段的动态质量，还提出了指数趋近率: 

B．改进的NFTSMC设计

      由(10)可以看出，系数的增加会加快收敛速度，但在接近滑模面时会引起抖振。因此，上述常规NFTSMC难以在收敛速度和抖振之间取得平衡。为了解决这一问题，在上述指数趋近定律的基础上，提出了一种适应滑模面和系统状态变化的NSMRL（新型滑模趋近率）：

      由(11)可以得到以下结论。当∣s∣增大时，即系统状态远离滑动面，系统状态按照变速趋近率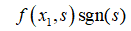和指数趋近率K1s两种速率达到滑模面。相反，当∣s∣减小时，K1s的指数逐渐趋近于零。在收敛时，变速趋近律项起着重要作用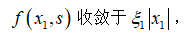，在滑模控制律的作用下，系统状态x1逐渐趋近于零。这表明当系统轨迹接近滑动面时，变速趋近项逐渐收敛于零以抑制抖振。因此，采用上述NSMRL设计的改进型NFTSMC不仅能抑制抖振，而且达到速率更快。将(11)中的NSMRL代入(7)的推导，并与(6)结合，得到改进后的NFTSM输出如下:

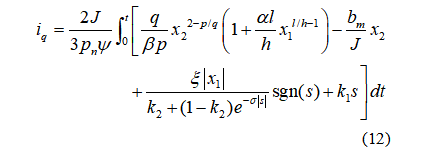
      由式(12)可以看出，滑模控制器中包含符号函数，这容易引起高频抖振。为进一步削弱抖振，采用双曲正切函数代替符号函数，如下所示:

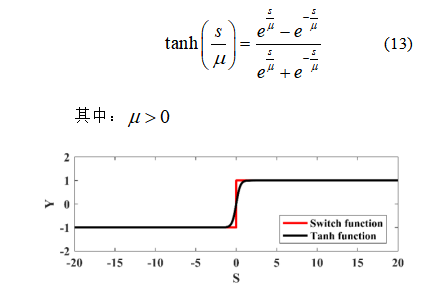
      常规开关函数和双曲正切函数的曲线如图所示。可以看出，与切换函数相比，双曲正切函数在实现滑模切换的过程中更加平滑。改进后的NFTSMC输出可进一步改写为：

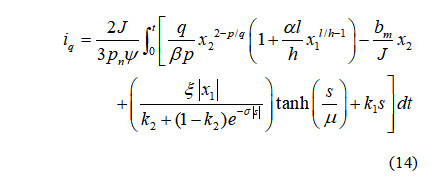
C．改进的NFTSMC稳定性分析

     结合相关参考文献，选择如下Lyapunov函数来证明改进后的NFTSMC的稳定性: 

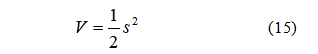
     对于任意给定s，存在μ > 0，且存在以下不等式: 

     结合6，11，14，15式可表示为：

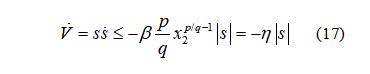
      由（17）式可知，当对于s≠0，V(t)∠ 0时，满足滑模收敛条件。假设系统滑模面初始条件，x(0)≠0,系统从S(0)≠0到S(0)=0的时间是Tr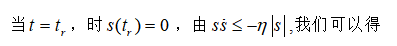，以下条件：

      当x2=0时x2并不处于稳态，系统不会总是停留在x1≠0,x2=0上，V不会一直等于0，所以从可以保证系统的状态变量从任何初始态出发都可以保证收敛到终端滑模面。

4  SMDO设计

      众所周知，SMC使用不连续项来限制扰动的影响，这本质上是一种开关控制。为了抑制各种干扰，SMC的开关增益被选择为一个很高的值，这可能会损害PMSM控制系统的性能。为了进一步提高永磁同步电动机的抗干扰性能，采用SMDO在线估计负载扰动，然后将估计的负载扰动作为前馈信号补偿转速控制器的输出。

     根据永磁同步电机的运动方程，可以建立滑模观测器的模型：

     对于，当J＞0，Bm＞0，SMDO渐进稳定时满足如下条件：

     因此，滑模面增益应该满足：

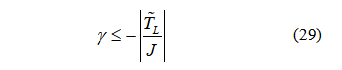
     当扰动观测器进入滑模面时，扰动观测器的误差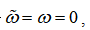,（24）可以转化为：

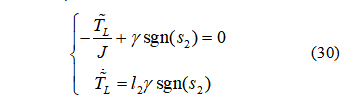
     进一步上式可以化为：

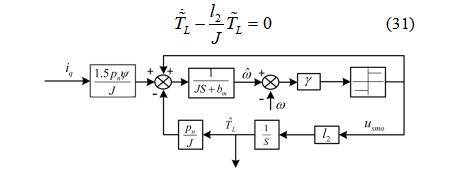
     通过稳定性理论研究，该微分方程状态稳定的

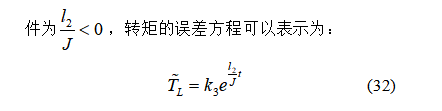
     K3是常数，负载扰动的估计误差随着时间推移不断减小，趋近滑模面的收敛速度由切换增益L2决定，适当的L2参数选择可以保证V∠0，转速的估计误差逐渐趋近于0，PMSM系统稳定，SMDO结构图如上图扰动前馈补偿表示为：

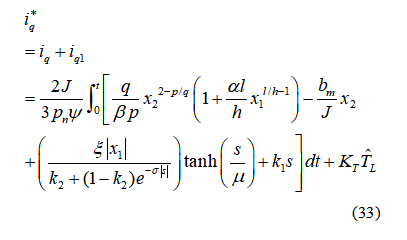
5  结论

      本文研究了一种非线性SMC技术，并将其应用于永磁同步电动机系统。为了抑制非奇异终端滑模控制（NFTSMC）的抖振现象，提高其跟踪性能，设计了基于新型趋近率（NSMRL）的改进型非奇异终端快速滑模控制器。此外，考虑到外部扰动对系统的不利影响，建立了负载扰动观测器(SMDO)来估计负载扰动，并用负载扰动估计值来补偿改进后的NFTSMC。最后，设计了一种将NFTSMC和SMDO相结合的复合控制器，进一步提高了PMSM驱动系统的扰动鲁棒性。仿真和实验结果均表明，该复合控制方法具有瞬态响应快、抗干扰能力强等特点。