基于频率自适应扰动观测器的PMSM无感控制技术-乔牧博士
2023-08-28
摘要:转子角可以根据永磁同步电机(PMSM)的定子磁链来估计。在静止参考系中,用电压和电流估计定子磁链中积分环节至关重要,但由于实际原因,积分过程中可能会出现干扰。本文提出了一种频率自适应扰动观测器,以消除定子磁链估计中的扰动,提高转子角估计的精度。
1 引言
基于PMSM的定子磁链,即使在零速度下,定子磁链也不会消失,除非转子磁链被定子电流完全抵消。然而,由于在普通驱动系统中不能直接测量定子磁链,因此如何测量或估计定子磁链是基于定子磁链的无传感器方法中的关键问题。
通常,定子磁链的估算基于(1),该公式由(2)中的定子电压方程导出。
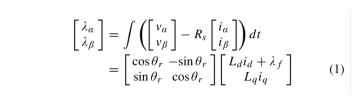
如(1)所示,在α-β框架中有两种方法来估计定子磁链,一种是基于电压积分,另一种是根据d-q磁链的坐标变换。前者称为电压模型法,后者称为电流模型法。虽然电流模型不能单独用于无传感器控制系统,但它可以补充电压模型的缺点。也就是说,虽然来自电压模型的估计通量即使在静止时有小误差也会发散,但电流模型不会引起同样的问题。然后,结合电流模型的电压模型已被广泛用于定子磁链估计。然而,当前模型需要几个参数Ld、Lq、λf、和θr。特别是由于θr的估计误差受总体参数的影响,当前模型容易受到参数变化的影响。
本文提出了一种新的扰动观测器来代替定子磁链估计的电流模型部分。该观测器的设计基于信号处理而非电机建模。详细地说,观测器根据其频率特性来消除通量估计中的不期望分量。该设计原则有望减轻当前模型的参数依赖性。
2 转子角的估算
PMSM的电压方程在固定参考系中给出如下[5]:
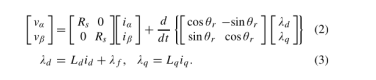
定子磁链可根据(1)通过积分计算,该积分基于(2)。当考虑(1)和(3)中的电流模型时,静止参考系中的定子磁链可以描述为:
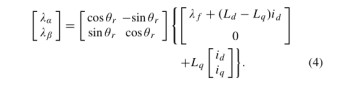
经过一些代数运算,(5)可以从(4)导出
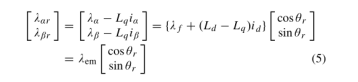
其中,如果Ld与Lq不相同,λem可以是虚拟磁链。无论显著性如何,λem都与转子轴对齐,称为d轴。λαr和λβr是λem在α−β框架中的分量。
考虑到(1)和(5),与转子角度相关的信息可以通过α−β框架中的电压和电流获得,因为(5)中的λα和λβ可以通过(1)中的积分计算。除非(5)中的λem根据运行条件变为零,否则转子角度可直接计算为
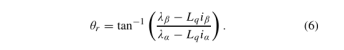
其中ωf表示定子磁链的转速。
3 磁链估计的扰动观测器
对于通过(6)计算转子角度,磁链估计至关重要。在这种估计中,不可避免地使用(1)中的积分。然而,积分器在信号处理中的应用可能会受到干扰。也就是说,如果没有额外的处理,α−β框架中估计的定子磁链可能包含一些扰动。这些干扰可能来自实际原因,例如积分器的初始化误差、传感器的脉冲噪声和数字系统中的量化误差。无论是什么原因,这些类型的干扰都应该被抵消,以便准确估计转子角度和速度[]。
A. 设计扰动观测器的状态方程
当λm表示α-β框架中定子磁链的大小时,通过实际系统中的积分估计的定子磁链可以建模为:
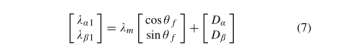
其中,λα1和λβ1表示基于(1)中积分的初始估计定子磁链,扰动用Dα和Dβ表示。此外,θf表示定子磁链角。
干扰主要是低频现象,可以通过阶跃信号模型来建模。此外,如果λm也假定为阶跃变化,则(7)的导数可以是:
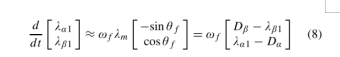
根据(8),估计定子磁通量的状态方程可导出为:
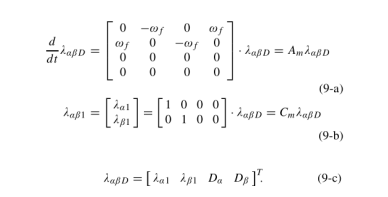
通过(9)中的Am和Cm可以很容易地确认线性系统是否可观察。由于(9)中的线性系统是可观察的,Luenberger观测器可以设计为:
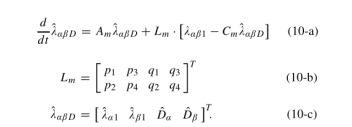
B. 干扰观测器的增益设置
(10)中的扰动观测器具有与ωf相关的自适应增益。对于增益设置,可以讨论观测器的内部传递函数,这些传递函数导出为(11)。
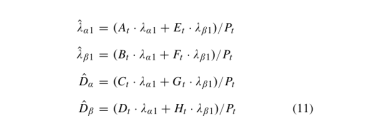
其中(11)中的所有传递函数都详细描述为:
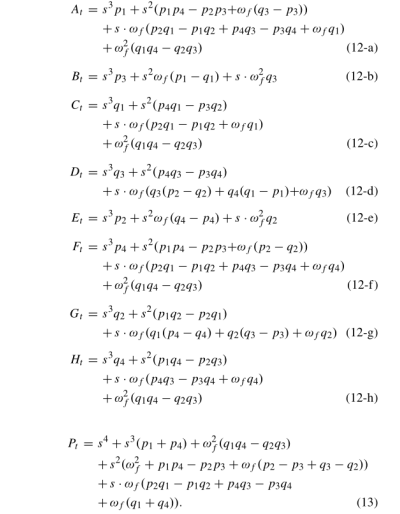
如(12)和(13)所示,传递函数依赖于ωf,ωf是定子磁链的角频率。如果ωf反转,则观测器的极点可能移动到右半平面,从而导致不稳定的操作。为了抵消频率反转的影响,观测器的增益可以根据以下获得:
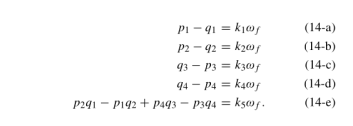
通过设置(14),ωf仅在传递函数的系数中以其平方的形式出现。也就是说,在一定速度下的极点和零点与在相反速度下的相同。通过仅考虑正情况来放置观测器极点。此外,可以采用(15)的条件使观测器结构在α−β框架中对称
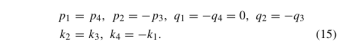
(13)的所有根,即观测器极点,都位于负实轴上的距离|ωf|处。从根本上讲,这是因为极点的固有频率应至少等于(7)中信号的最高频率,并且可以滤除一些大于ωf的谐波。观测器增益最终确定为
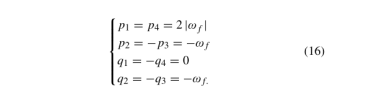
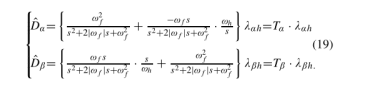
当使用(16)中的增益时,与干扰相关的传递函数如下:
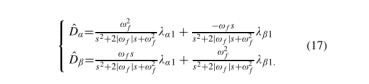
由(5)得,α−β磁链可以改写为:
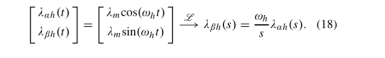
基于(17)和(18),所提出的观测器对α−β磁链的频率响应可以用:
4 结语
为了提高基于永磁同步电机定子磁链模型的无传感器控制方法的性能,本文提出了一种频率自适应扰动观测器。建立了观测器的状态方程,并详细讨论了如何在考虑永磁同步电机转速反转的情况下设置观测器增益。此外,提出了几个辅助模块,以将所提出的观测器集成到无传感器控制系统中。.
