摘 要： 本文简要介绍了一种基于速度的线性化速度形式非线性模型预测控制（NMPC）方案。这种方法的主要特点是在存在干扰时内置无偏移控制，跟踪分段常数（可能无法访问的参考信号）以及简单的实现，因为不需要对所有平衡进行参数化。此外，速度形式的模型可以表示为准线性参数变化（准LPV）模型，该模型存在有效的在线优化算法。所提出的方法在2自由度机器人机械手上进行了实验验证，并强调了其功能和效率。

     关键词：线性化技术；非线性控制系统；预测控制

0 引言 

      速度算法或速度形式长期以来一直用于PID控制器的实现。它也被用于控制非线性系统，例如，在中，它被用于实现增益调度控制器。虽然基于速度的线性化的概念是在中作为分析工具引入的，但与此同时，这种线性化已成为一种建模技术，这导致控制器实现类似于的速度算法。在速度形式MPC的背景下，大部分文献都集中在LTI系统上。在 中，给出了一个速度形式的 MPC 教程，它涉及其实现的所有一般方面。技术报告 中讨论了 LQR 问题的速度，其中简要讨论了在处理无法到达的设定点时有限水平 LQR。在中提出了使用MPC以速度形式跟踪恒定参考信号的问题;在那里，还以类似于的方式处理了无法访问的引用问题，后者使用标准 MPC考虑相同的问题。在这些方法中，通过使用偏移成本函数来处理无法到达的设定点，该函数惩罚虚构的、可到达的设定点与实际设定点的偏差。同样的想法在中扩展到非线性系统。非线性速度形式MPC已在中用于控制涡扇发动机间隙。鼓励使用基于速度的线性化，并突出其优点，但没有进行稳定性分析。同样，基于速度的线性化用于获得状态相关模型，该模型用于应用于中应用于 pH 过程的非线性 MPC 的神经网络近似。

      在本文中，我们重点跟踪非线性系统的分段常数、不一定可到达的参考信号。所提出的方法可以理解为与中提出的方法平行的速度形式，这就是为什么我们经常引用它的原因。可以看出，速度形式不仅在存在扰动时具有内置的无偏移控制，而且由于不需要对所有平衡状态和输入进行参数化而变得更加简单：所有平衡都映射到原点。此外，它自然导致非线性模型的准线性参数变化（准LPV）形式，适用于高效的在线算法，例如qLMPC算法。

      通过使用基于速度的线性化来获得模型，该模型在由状态和输入的时间导数定义的切线空间中是线性的，从而实现速度形式向非线性系统的扩展。这个模型在整个状态空间上也是精确的，它不像通常的雅可比线性化那样局限于均衡点。

      提出的方法的实验应用，其中提出了使用基于速度的准LPV模型的想法，但没有稳定性证明，并在具有非线性状态约束（障碍物）和线性输出（关节空间）的2自由度机器人机械手上进行了说明。

      本文组织结构如下。第二部分设置了这个问题，并通过基于速度的线性化引入了非线性速度形式。第三节介绍了MPC问题，并给出了主要的收敛结果。第四节简要回顾了qLMPC算法作为解决非线性优化问题的推荐方法和最后结束语。

1 问题设置

考虑以下形式的非线性连续时间模型

                  x=f(x,u)

                  y=h(x)

其中x∈Rn，x∈Rm和y∈Rl我们假设f(.)和h(.)都是(x,u)的可微函数；此外，在输入和状态受约束，即x(t)∈X和u(t)∈U。我们希望设计一种最优状态反馈控制律，它在跟踪给定的恒定参考信号时考虑约束。最后，要设计速度形式MPC，以提供任意设定点的无偏移跟踪Ysp，而无需参数化所有可容许平衡，因为它们都映射到速度空间的原点（x=0和u=0）。

      为了获得速度形式的模型，我们使用了基于速度的线性化方法，与雅可比线性化相比，该方法具有精确（即，在整个状态空间中有效）和易于计算的优点。作为副产品，获得了状态相关线性模型，该模型可以直接表示为准LPV模型。因此，可以利用模型的（准）线性来有效地解决MPC定律所带来的非线性优化问题。 

1.1基于速度的线性化和速度F型

     基于速度的线性化通过相对于时间微分状态和输出方程来计算。

      模型（2）在状态导数方面是线性的，状态空间矩阵现在是状态相关的。关于（x和u）的稳态值的信息在微分过程中丢失；为此，该模型用l个积分器进行扩充，以获得与速度形式相关的等效状态：

      采样时刻Ke的离散化信号x(t)。对于LPV系统离散化的几种方法，可以通过多种方法获得离散化速度模型，或者对于基于速度的线性化系统，可以通过获得离散化方法。我们将集合定义为可容许参数值的集合。

2 跟踪的MPC

     我们首先陈述模型的假设。

     假设1：

    1）模型（4）是可稳定的∀ρ∈P。

    2） l≤m，即跟踪输出的数量小于或等于输入的数量。

    3） 系统具有连续的强制平衡轨迹（即，系统没有孤立的强制平衡）。并且相应地，在N个步骤中可达到的稳定状态集合为。

     注意，这些集合可以理解为存在视线的可达到稳态输出的集合，这本身就是一组可接受的稳态输出。

     调谐矩阵Q1和R是正定的，Q2是半正定的，ysp是设定点。中注意到，相对于实际设定点（在这种情况下为ysp）惩罚误差的阶段成本比相对于人工设定点（ys）惩罚误差更有意义，因为人工设定点通常是这样做的，因为后者可能会因瞬变扰动而改变，从而导致过度的控制动作和潜在的性能损失。

      要在线解决的优化问题如下我们考虑成本函数注意，约束保证对应于的终端状态是稳定状态，这在设定点跟踪策略中经常被假设。将问题的解的输入增量的最优序列定义为U*=（U*0，U*1，…，U*N−1），后退视界原理的应用将隐式控制律定义。

      接下来，我们将介绍本文主要结果。

      定理1：假设假设1成立，并考虑标量a＞0的偏移惩罚T=αΟ1。给定一个设定点Ysp，从优化问题的解中导出的控制律从可行状态开始稳定系统（4），是递归可行的，并使输出收敛到以下之一。

      证明分为三个步骤。步骤I建立了递归可行性，步骤II证明了成本函数的单调性，从而证明了稳定性，步骤III证明了与优化相容的唯一平衡点是定理1中第1项和第2项所列的平衡点。步骤I和步骤II是MPC文献中的标准步骤，此处显示了针对速度算法的适当修改，以确保完整性。步骤III紧跟，其中使用凸性参数证明了收敛到最佳稳态。

      第一步：假设初始状态的可行性，问题（7）解的最优输入增量序列为U*k=（U*k，U*k+1，…，U*k+N−1）；在k+1处的可行、可能次优序列

       U*k+1=（U*k+1，U*k+2，...U*k+n-1,0）

      通过从时间步骤k移动解并在末尾附加uk+N=0，即设置uk+N=uk+N−1获得。在约束条件下，状态是强制平衡；因此，保持相同的输入将使系统保持在稳定状态并且是可行的。

      第二步：假设稳态问题

      在每个时间步在线求解（下标k表示它是在时间k计算的最优解），并假设中的被设置为Ys=y。注意，这是可行的，因为稳态问题被限制为NY。显然，在时间步骤k+1，（8）的可行（可能次优）解为Yk+1=Yk。考虑到这一点以及步骤I中给出的时间步长k+1的可行输入序列，可以根据处的最优成本获得k+1处的成本函数的可行（可能次优）值（回想一下，从步骤I中，k+1处可行输入序列是通过移动k处的最佳序列并在末尾附加u＝0而获得的）.

      注意，问题的解决方案不会通过将终端约束代入成本函数而改变。这样做消除了问题中的变量，从而避免了的在线解决方案；它还将偏移函数转换为终端成本。

      步骤三：该步骤基于凸性参数；通过矛盾，证明了在定理1中第2项的意义上，不可能收敛到非最优的可行稳态。假设y*是最优稳态输出，使得成本函数最小化，但存在。考虑到Y的财产和假设1中的第三项， Y是可行的稳态。

     请注意，左手边等于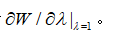

     由于这是正的，并且从W的连续性来看，存在λ<1，因此W，因此jK小于j*K，这与j*K的最优性相矛盾。因此，根据定理1中的第1项和第2项，算法收敛到最佳稳态。

      备注2：由于分析基于离散化模型（4），因此给出了该模型的稳定性和收敛性保证。结果是否扩展到原始连续时间系统（1）取决于离散化方法。

3 MPC的准线性

      如第二节所述，使用基于速度的线性化可以实现准线性化，从而有效地解决优化问题。为此，在此，我们提出了准LPV系统的qLMPC算法或MPC。这是一种迭代算法，它在每个采样间隔处求解一系列二次规划，其中每次调度轨迹在前一个解处冻结，基本上将准LPV模型（4）变为线性时变（LTV）模型。该过程如算法1所示，其中（Pk）如本页底部所示，是一个选择器函数，类似于选择器矩H，用于预测范围内的所有未来状态和输入。

      注意，算法1类似于LTV预测控制，其中沿着预先计算的参考或种子轨迹进行线性化，但它提供的优点是不需要潜在的与系统动力学兼容的轨迹的复杂计算，并且使用精确的准LPV模型（在这种情况下通过速度线性化获得）代替雅可比线性化。

      算法1的停止标准可以务实地选择为预定义的迭代次数，否则两个连续迭代的预测状态之间的差的范数小于预定义的公差，即||X l−X l−1||<。算法1的收敛性分析概述见。

      在闭环性能和数值效率方面，与最先进的方法相比，基于实时迭代算法，qLMPC被证明与ACADO相当，并且基于内部点求解器IPOPT，优于CasADi（在计算效率方面）。基准比较见。注意，虽然所提出的速度算法特别适合于与qLMPC一起使用，但它也可以与任何上述方法或任何其他非线性模型预测控制（NMPC）方法一起使用，因为定理1中的结果没有对如何解决优化问题做出任何假设。

4 实验验证

      在本节中，我们在前面中所述的2自由度机器人操纵器上实验说明了速度算法；然而，与相反现在定义为端效应器的笛卡尔坐标，这是一个常见的实际问题，它使输出成为状态的非线性函数。实际上，在这些条件下，给出了机器人操纵器的非线性模型

其中，分别为关节角度、速度和加速度；M是惯性矩阵，c是科里奥利力矢量，g是重力矢量，τ是施加的扭矩，是摩擦扭矩，其仅建模为粘性。模型矩阵由下式给出

     其中集中参数b1，b9取自，列于表I中。进行速度线性化，使模型成为（2）的形式，其中状态向量由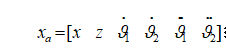给出。随后使用前向欧拉方法对速度模型进行离散化，采样时间为ts=0.01s；离散系统的状态向量用表示。考虑了两种测试场景，对应于定理1中列出的两种情况；在测试1中，设定点i＝1，2，3，它们依次应用，都是可到达的，而在测试2中，引入了输出约束，使得设置点ysp，1不可到达。两个测试的设定值相同

      两个实验中闭环响应的时域，显然，测试1的结果与预期一致，因为两个输出都达到了预期的稳定状态；然而，在测试2中，由于输出限制，未达到设定值。为了说明这种情况下闭环的收敛财产，xz平面的响应以及输出约束和集||y−ysp，1||2T。根据定理1，输出应该收敛到可到达集合NY（具有视线的最佳点）内的最佳值，在这种情况下，由集合首先与对角线相交的点给出。

      稳定性通过终端速度约束来实现，这意味着预测的轨迹应该在地平线末端达到稳定状态。在t∈[20 20.05]s（即，发生第一次参考变化时）的预测速度轨迹。

4 结论

      本文提出了一种用于非线性MPC的速度算法，其中基于速度的线性化用于获得速度形式的模型。该方案具有以下特点：无需扰动模型即可实现无偏移控制；不需要对所有平衡状态和输入进行（可能复杂的）参数化，因为它们都映射到原点；所提出的方案能够跟踪可达和不可达的设置点；并且它基于同样易于计算的精确线性化。另一方面，它的主要缺点是，除非引入uk−1的进一步状态增强，否则不能在成本函数中直接惩罚输入；它需要状态的速度作为反馈信号；如果它们不能够可用，则观察者通过微分滤波器进行必要的或数值微分。这不是该算法独有的，而是大多数基于速度的方法共享的特征。基于速度的线性化的使用自然会导致模型动力学的准LPV表示，并易于使用计算效率高的算法实现。